 想像地図研究所 (IML)
想像地図研究所 (IML)
このサイトは、芸術作品としての架空の土地の地図をメインテーマに扱ったサイトです。
初めての方は、こちらをご覧ください。
 想像地図研究所 (IML)
想像地図研究所 (IML)このサイトは、芸術作品としての架空の土地の地図をメインテーマに扱ったサイトです。
初めての方は、こちらをご覧ください。
最長片道切符は、発行できる片道切符のうち、距離が最も長いもののことです。
様々な鉄道事業者に関して最長片道切符を考えることができますが、ここでは(日本の)JRの最長片道切符について考えてみましょう。
※この文章は西九州新幹線の開通前に書かれたものです。日田彦山線の部分廃止等も考慮した計算を今後実行予定です。
JRの切符は、発駅(スタート)と着駅(ゴール)が同じでも、途中の経路が異なれば運賃は異なります。「最短の経路で発行される」というイメージがあるかもしれませんが、それは大都市近郊区間内の特例です。原則は経路通りに運賃を計算します。
そして、どのような乗車券なら発行できるかというと、その条件は「同じ駅を2回以上通過しない」です。
まず第一に思いつくのは、一本道の切符です。この形の切符を「1の字型」もしくは「L型」といいます。
しかし、一本道以外の形の切符も発行することができます。「同じ駅を2回以上通過しない」という条件ですから、ぐるっと一周して、出発した駅に戻ってくるような切符もOKです。この形の切符は「0の字型」もしくは「O型」といいます。
もう1つは、途中で通過した駅に到着してそこで終わりという切符です。「6の字型」もしくは「P型」といいます。同じ駅を2回通っているように見えますが、2回目はそこで終わり(通過していない)のでOKなのです。
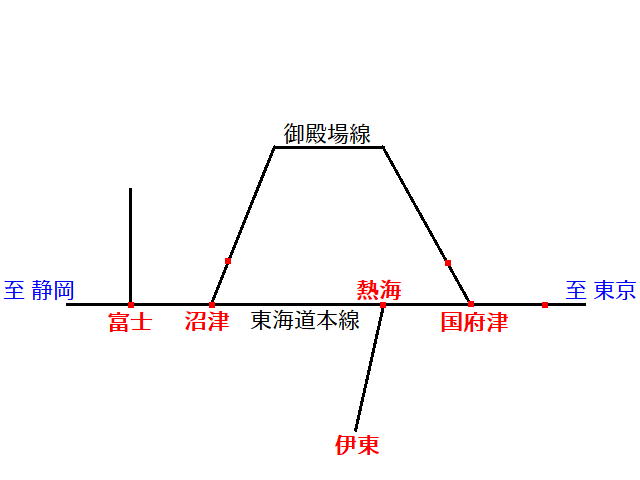
上図の例では、
・1の字型(L型)の例:富士から東海道本線でまっすぐ国府津に
・0の字型(O型)の例:沼津から東海道本線で国府津に至り、そこから御殿場線で沼津まで
・6の字型(P型)の例:富士から東海道本線で沼津を経て国府津に至り、そこから御殿場線で沼津まで
ただし、沼津から御殿場線で国府津に行き、そこから東海道本線で富士までという切符は、沼津を2回通過しているため条件を満たしていません。
「6の字型」はOKですが、逆方向の「9の字型」はNGです。
やっと本題です。最長片道切符は、「同じ駅を2回以上通過しない」という条件を満たす切符のうち、距離が最も長いもの、ということになります。
これまで、様々な人々が最長片道切符の経路を考察してきました。1961年に東大旅行研究会のメンバーがこの問題を考えたのが最初と言われています。彼らは、全国を地域ブロックに分割し、各ブロックごとに総当たりで最長ルートを求め、これを合算するという方法で行ったようです。しかし、電卓すら普及していない時代に行われたため、「本当にそれが最長なのか?」という確証が得られるものではありませんでした。実際、彼らが求めたルートは実は最長ではなかったと近年になって判明しています。
従って、最長片道切符の算出は、厳密にそのルートが最長であることが、数学的に示せる方法でなければなりません。しかし、コンピューターに解かせる場合、JRには5000ほどの駅があるので、発駅(スタート)と着駅(ゴール)の組み合わせだけでも5000×5000=2千5百万通りあることになります。そのそれぞれについて、膨大な数の経路の組み合わせがあるため、計算が終わるのに何億年もかかるという事態になりかねません。
そのことは、YouTubeにある「フカシギの数え方」という動画を見ていただくと分かると思います。
そこで、上記の動画の最後で触れられている「最先端のアルゴリズム」を使って最長片道切符の経路を算出してみましょう。[注釈1]
Graphillionという最先端のアルゴリズムを使って、最長片道切符の経路を算出しましょう。
日本列島を縦横無尽に走るJRの路線の形状に注目すると、以下のことが分かります。
・本州と北海道を結ぶ経路は1本しかないので
→ 本州から北海道に入って再び本州に戻る片道切符は発行できない
・本州と四国を結ぶ経路も1本しかない
→ 本州から四国に入って再び本州に戻る片道切符は発行できない
・本州と九州を結ぶ経路は2本あるように見えるが、この区間で新幹線と並行する在来線は同一の路線として扱う
→ 本州から九州に入って再び本州に戻る片道切符は発行できない
九州と四国では路線の長さが九州の方が長いため、最長片道切符の経路は「北海道→本州→九州」or「九州→本州→北海道」という経路であると推測できます。厳密には、本州内だけで回った場合の最長経路よりも、「北海道→本州→九州」or「九州→本州→北海道」の最長経路が長いことを示す必要がありますが、とりあえず今は「北海道→本州→九州」or「九州→本州→北海道」という前提条件で考えてみることにします。
経路が
・北海道→本州→九州
・九州→本州→北海道
のどちらかという前提で考えるため、北海道・本州・九州の3つに問題を分割して考えることができます。
まず、本州内の最長経路について考えてみます。
本州の分岐駅間の距離を書いた路線データを用意します。BRTは利用不可という前提で計算します。もちろん三江線廃止後のデータです。
なお、経路特定区間に関しては、中間に分岐駅がない場合は短い方のみをデータに掲載し、長い方はデータから除外します。
('東京', '品川', 6.8),
('品川', '川崎', 11.4),
('川崎', '鶴見', 3.5),
('鶴見', '東神奈川', 5.3),
('東神奈川', '横浜', 1.8),
('横浜', '大船', 17.7),
…
スタートが北海道でゴールが九州(もしくはその逆)なので、本州内のルートは、新青森から下関へ至る1の字型の最長経路を求めれば良いことになります。
スタートとゴールが固定されているため、盲腸線はデータから除外します。
from graphillion import GraphSet
universe = [
('東京', '品川', 6.8),
('品川', '川崎', 11.4),
('川崎', '鶴見', 3.5),
('鶴見', '東神奈川', 5.3),
('東神奈川', '横浜', 1.8),
('横浜', '大船', 17.7),
…
…
]
GraphSet.set_universe(universe)
paths = GraphSet.paths('新青森', '門司')
for path in paths.max_iter():
path # 最長経路を表示
break # break しないと、複数のパスが降順で取り出される
このコードを実行すると、以下の結果が得られます。[▼結果を表示する]
はい。残念ながらGraphillionは仕様上、通る順番で出てきません。そこで、ExcelVBAで通る順番に並べ替えるプログラムを書いて、正しい順番に書き換えたのが以下になります。
川部→東能代→追分(秋田)→秋田→余目→坂町→米沢→北山形→羽前千歳→新庄→横手→大曲→盛岡→新花巻→花巻→北上→一ノ関→古川→小牛田→前谷地→石巻→高城町→仙台→福島(福島)→岩沼→いわき→郡山(福島)→会津若松→新津→東三条→長岡→燕三条→新潟→吉田→柏崎→宮内→越後川口→飯山→糸魚川→松本→長野→佐久平→高崎→越後湯沢→渋川→新前橋→小山→宇都宮→宝積寺→安積永盛→上菅谷→水戸→友部→我孫子→成田→香取→松岸→成東→大網→木更津→蘇我→南船橋→市川塩浜→東京→品川→代々木→御茶ノ水→神田→秋葉原→錦糸町→西船橋→新松戸→日暮里→赤羽→田端→池袋→新宿→西国分寺→武蔵浦和→南浦和→大宮→熊谷→倉賀野→高麗川→拝島→立川→府中本町→武蔵小杉→尻手→浜川崎→武蔵白石→浅野→鶴見→東神奈川→横浜→桜木町→大船→茅ヶ崎→国府津→沼津→富士→甲府→八王子→橋本(神奈川)→新横浜→小田原→熱海→三島→静岡→豊橋→辰野→岡谷→塩尻→多治見→金山→名古屋→亀山→松阪→多気→和歌山→高田(奈良)→奈良→王寺→久宝寺→天王寺→今宮→西九条→大阪→京橋→放出→木津→柘植→草津→山科→近江塩津→米原→大垣→岐阜→美濃太田→富山→新高岡→金沢→越前花堂→敦賀→綾部→京都→新大阪→西明石→兵庫→尼崎→谷川→福知山→和田山→鳥取→東津山→姫路→相生→東岡山→岡山→津山→新見→総社→倉敷→福山→三原→広島→塩町→備後落合→備中神代→伯耆大山→米子→宍道→益田→新山口→宇部→居能→雀田→小野田→厚狭→長門市→幡生→門司
距離 7595.1 km
まず、北海道に着駅(ゴール)がある場合を考えます。
本州→北海道 という順で移動できる必要があるので、北海道内の経路の入口は新青森に固定されます。ゴールはどこになるかが未知です。
ですが、どの駅もゴールになる可能性があるわけではありません。ゴールになる可能性がある駅は、以下に絞られます。
・終端駅(行き止まりの駅)
・分岐駅(経路全体が6の字型になる場合もあるので、1度通過した分岐駅がゴールになる可能性もあります)
従って、ゴールなる可能性がある全ての駅について、最長を求め、その中で最も長いものが求める答えということになります。北海道には8個の終端駅と18個の分岐駅があるので、頑張って計算を26回すれば答えは出てきます。出てきますが、わざわざ26回計算するのは大変なので、データを工夫しましょう。
その方法は、路線データに「仮想終点」を追加することです(この方法はSWA様にヒントを頂いた方法を少し応用しました)。
ゴールになる可能性がある全ての駅と仮想終点までの間に「仮想の線路」があるというデータを作ります。仮想の線路の長さは0kmとしておきます。その上で、新青森から仮想終点に至る最長経路を求めると、「新青森→…→…→仮想終点」という経路の中で最長のものが出てきます。そのとき、仮想終点の1つ手前の駅が「本当の着駅」になっているはずです。
よって、出てきた答えから仮想終点を取り除けば、求めている答えが出てくるわけです。
ですが!!
この方法には重大な落とし穴があります。経路が6の字型だった場合、正しい経路が出てきません。
Graphillionが計算できるのは、「スタートとゴールを含めて、同じ地点を2回通らない経路」です。しかし一方で、JRの切符の発行条件は、先述したとおり、「同じ駅を2回以上通過しない」という条件です。6の字型は「ゴールの駅だけは2回訪れる」ため、上手くGraphillionでは計算できません。そこで、もう1つの工夫を用意します。
簡単な例として、このような分岐駅を考えてみます。
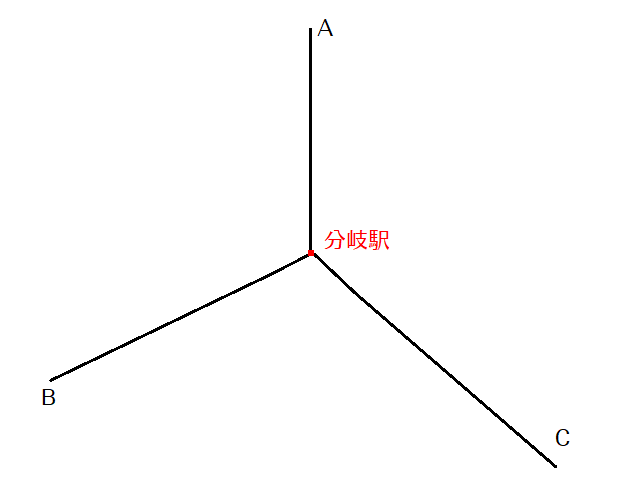
上記の路線の場合、分岐駅からA・B・Cという3つの駅がある方向に向かって線路が延びています。
この場合、もし最長経路が「A→分岐駅→C→…→…→B→分岐駅」という経路だった場合、正しく計算されません。
これに、ダミー駅を追加します。
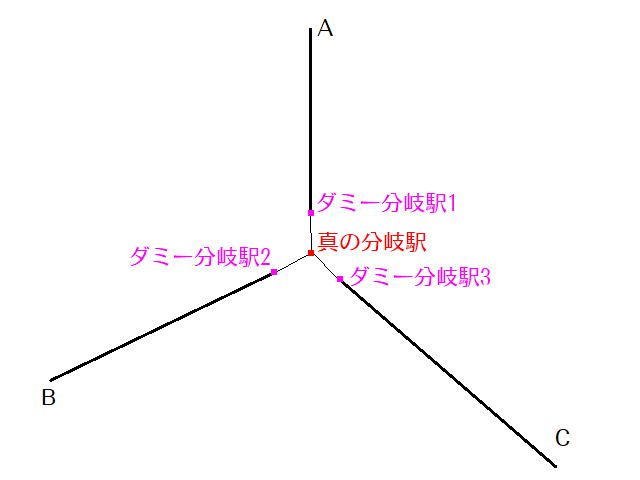
3-5で「仮想終点」を考えたことを思い出してみましょう。仮想終点とつながる仮想線路は、真の分岐駅ではなく、ダミー分岐駅のほうに繋げるのです。
そうすると、もし最長経路が「A→分岐駅→C→…→…→B→分岐駅」という経路だった場合、Graphillionでの結果は「A→ダミー分岐駅1→分岐駅→ダミー分岐駅3→C→…→…→B→ダミー分岐駅2→仮想終点」という経路が出てきます。一方、ダミー分岐駅2からさらに進もうとすると、既に通過した真の分岐駅を通らないと進めません。従って、このダミー分岐駅を導入すると、6の字型の経路は正しく拾われます。そして9の字型の経路は正しく棄却されます。
なお、北海道への入口は新青森に固定されているため、ダミー分岐駅が入口になってしまい9の字型経路を出してくるということは起きません。
次に、北海道に発駅(スタート)がある場合を考えます。
北海道→本州 という順で移動できる必要があるので、北海道内からの出口は新青森に固定されます。今度は、スタートがどこになるかが未知です。
ですが、どの駅もスタートになる可能性があるわけではなく、可能性がある駅は以下に絞られます。
・終端駅(行き止まりの駅)
・分岐駅の隣の駅(9の字型はNGなので、9の字から1駅だけ減らすと発行条件を満たすようになる)
北海道がゴールになる場合は、「仮想終点」という工夫を取り入れました。スタートになる場合は、逆に「仮想起点」を取り入れます。スタートになる可能性がある全ての駅と仮想起点までの間に「仮想の線路」があるというデータを作ります。その上で計算すると、「仮想起点→…→…→新青森」という経路の中で最長のものが出てきます。そのとき、仮想起点の1つ次の駅が「本当の発駅」になっているはずです。
なお、分岐駅の隣の駅がスタートになることはあっても、分岐駅がスタートになることはないので、この場合はダミー分岐駅は不要です。
3-4~3-6で考えた工夫を取り入れて、北海道内と九州内の最長経路を算出してみましょう。
ただし、長期運休となっており廃止が事実上決定している「日高本線 鵡川以遠」と「根室本線 富良野-新得」は利用できないという前提で経路を算出しました。
a. 北海道がゴールになる場合の経路 (距離 1529.7 km)
新青森1→奥津軽いまべつ→木古内→新函館北斗3→新函館北斗Y→新函館北斗2→仁山→大沼1→大沼Y→大沼2→大沼公園→駒ヶ岳→森1→森Y→森2→石谷→中ノ沢→長万部1→長万部Y→長万部2→二股→小樽→琴似→桑園1→桑園Y→桑園2→札幌→苗穂→白石(北海道)1→白石(北海道)Y→白石(北海道)2→厚別→上幌向→岩見沢1→岩見沢Y→岩見沢2→峰延→滝川1→滝川Y→滝川3→東滝川→野花南→富良野1→富良野Y→富良野3→学田→神楽岡→旭川2→旭川Y→旭川3→旭川四条→新旭川1→新旭川Y→新旭川3→南永山→網走→遠矢→東釧路3→東釧路Y→東釧路1→釧路→十勝清水→新得3→新得Y→新得1→トマム→新夕張2→新夕張Y→新夕張1→滝ノ上→川端→追分(北海道)2→追分(北海道)Y→追分(北海道)1→南千歳3→南千歳Y→南千歳1→植苗→沼ノ端1→沼ノ端Y→沼ノ端2→苫小牧2→苫小牧Y→苫小牧1→青葉→東室蘭2→東室蘭Y→東室蘭1→本輪西→静狩→長万部3
b. 北海道がスタートになる場合の経路 (距離 1521.1 km)
二股→小樽→琴似→桑園1→桑園Y→桑園2→札幌→苗穂→白石(北海道)1→白石(北海道)Y→白石(北海道)2→厚別→上幌向→岩見沢1→岩見沢Y→岩見沢2→峰延→滝川1→滝川Y→滝川3→東滝川→野花南→富良野1→富良野Y→富良野3→学田→神楽岡→旭川2→旭川Y→旭川3→旭川四条→新旭川1→新旭川Y→新旭川3→南永山→網走→遠矢→東釧路3→東釧路Y→東釧路1→釧路→十勝清水→新得3→新得Y→新得1→トマム→新夕張2→新夕張Y→新夕張1→滝ノ上→川端→追分(北海道)2→追分(北海道)Y→追分(北海道)1→南千歳3→南千歳Y→南千歳1→植苗→沼ノ端1→沼ノ端Y→沼ノ端2→苫小牧2→苫小牧Y→苫小牧1→青葉→東室蘭2→東室蘭Y→東室蘭1→本輪西→静狩→長万部3→長万部Y→長万部1→中ノ沢→石谷→森2→森Y→森1→駒ヶ岳→大沼公園→大沼2→大沼Y→大沼1→仁山→新函館北斗2→新函館北斗Y→新函館北斗3→木古内→奥津軽いまべつ→新青森1
c. 九州がゴールになる場合の経路 (距離 1244.4 km)
西小倉Y→西小倉3→南小倉→城野1→城野Y→城野2→安部山公園→西大分→大分3→大分Y→大分4→牧→宮崎→南宮崎1→南宮崎Y→南宮崎2→加納→三股→都城1→都城Y→都城3→日向庄内→鶴丸→吉松3→吉松Y→吉松2→栗野→日当山→隼人1→隼人Y→隼人3→加治木→鹿児島→鹿児島中央3→鹿児島中央Y→鹿児島中央1→広木→川内(鹿児島)→新水俣→新八代3→新八代Y→新八代1→千丁→松橋→宇土2→宇土Y→宇土1→富合→西熊本→熊本2→熊本Y→熊本1→上熊本→瀬高→筑後船小屋2→筑後船小屋Y→筑後船小屋1→羽犬塚→荒木→久留米2→久留米Y→久留米4→久留米高校前→筑後大石→夜明1→夜明Y→夜明3→今山→池尻→田川後藤寺2→田川後藤寺Y→田川後藤寺3→船尾→上三緒→新飯塚3→新飯塚Y→新飯塚1→浦田→東水巻→折尾4→折尾Y→折尾2→水巻→九産大前→香椎1→香椎Y→香椎2→千早→箱崎→吉塚1→吉塚Y→吉塚3→柚須→原町→長者原3→長者原Y→長者原4→門松→筑前大分→桂川1→桂川Y→桂川3→上穂波→筑前山家→原田3→原田Y→原田1→天拝山→竹下→博多3→博多Y→博多4→新鳥栖1→新鳥栖Y→新鳥栖4→肥前麓→鍋島→久保田1→久保田Y→久保田2→牛津→肥前山口1→肥前山口Y→肥前山口2→肥前白石→東諌早→諫早1→諫早Y→諫早3→岩松→ハウステンボス→早岐3→早岐Y→早岐1→三河内→大町(佐賀)→肥前山口3
d. 九州がスタートになる場合の経路 (距離 1239.3 km)
肥前白石→東諌早→諫早1→諫早Y→諫早3→岩松→ハウステンボス→早岐3→早岐Y→早岐1→三河内→大町(佐賀)→肥前山口3→肥前山口Y→肥前山口1→牛津→久保田2→久保田Y→久保田1→鍋島→肥前麓→新鳥栖4→新鳥栖Y→新鳥栖1→博多4→博多Y→博多3→竹下→天拝山→原田1→原田Y→原田3→筑前山家→上穂波→桂川3→桂川Y→桂川1→筑前大分→門松→長者原4→長者原Y→長者原3→原町→柚須→吉塚3→吉塚Y→吉塚1→箱崎→千早→香椎2→香椎Y→香椎1→九産大前→水巻→折尾2→折尾Y→折尾4→東水巻→浦田→新飯塚1→新飯塚Y→新飯塚3→上三緒→船尾→田川後藤寺3→田川後藤寺Y→田川後藤寺2→池尻→今山→夜明3→夜明Y→夜明1→筑後大石→久留米高校前→久留米4→久留米Y→久留米2→荒木→羽犬塚→筑後船小屋1→筑後船小屋Y→筑後船小屋3→新大牟田→新玉名→熊本3→熊本Y→熊本2→西熊本→富合→宇土1→宇土Y→宇土2→松橋→千丁→新八代1→新八代Y→新八代3→新水俣→川内(鹿児島)→広木→鹿児島中央1→鹿児島中央Y→鹿児島中央3→鹿児島→加治木→隼人3→隼人Y→隼人1→日当山→栗野→吉松2→吉松Y→吉松3→鶴丸→日向庄内→都城3→都城Y→都城1→三股→加納→南宮崎2→南宮崎Y→南宮崎1→宮崎→牧→大分4→大分Y→大分3→西大分→安部山公園→城野2→城野Y→城野1→南小倉→西小倉3→西小倉Y
3-7で北海道と九州の経路が分かりました。日本全体の最長経路は「北海道→本州→九州」か「九州→本州→北海道」のどちらかでしたので、このうち長い方が求めるべき最長経路ということになります。どちらの場合も本州内の経路1の字型なので長さは変わりません。
よって「北海道スタート + 九州ゴール」と「九州スタート + 北海道ゴール」のうち、距離の長い方が答えです。
前者は1521.1+1244.4=2765.5
後者は1239.3+1529.7=2769.0
よって、九州の肥前白石をスタートして北海道の長万部でゴールというのが、最終的な答えです。
その距離は、九州 1239.3 km + 本州7595.1 km + 北海道 1529.7 km = 10364.1 km
既に知られているものは、稚内がスタート、肥前山口がゴールというものでしたが、日高本線の鵡川以遠・根室本線の富良野-新得・三陸のBRTを利用不可という条件を設定したところ、「肥前白石→長万部」という見慣れない結論が出てきました。
ちなみに、データにおおさか東線の「新大阪-鴫野」を足して計算しても最長経路は変化しませんでした。
今回の最長片道切符経路の算出は、「北海道→本州→九州」か「九州→本州→北海道」のどちらかであるという前提条件を設定したため、厳密に言えばこれは「北海道→本州→九州または九州→本州→北海道という経路の中で最長と数学的に示せる経路」です。「本当は本州の中だけで回った方が長いのでは?」という可能性を否定できていません。
より厳密な答えを出すためには、日本全国の路線網に対して、仮想起点・仮想終点・ダミー駅を設定した路線データを用いて計算を実行するべきなのです。筆者はそれも行いましたが、メモリ不足でGraphillionが強制終了するという事態が発生しました。すなわち、筆者のPCの能力ではそれはできないということになるため、今回はこれでもって結論としました。
また同様に、将来四国新幹線が開業し、和歌山と徳島、および松山と大分が結ばれた場合、本州と四国を結ぶ場所が2箇所になり、九州と四国も直接結ばれるため、今回のように「スタートとゴールはそれぞれ北海道と九州もしくはその逆で、本州は通り抜けるだけ」という前提条件を置くことができなくなります。そのため、厳密性を保ったまま経路を算出するためには、更なる工夫が必要となるでしょう。
なお、今回は日本のJRの最長片道切符経路を算出しましたが、将来的に「想像地図世界の最長片道切符」についても同じ方法で計算することを考えております。
当サイトは架空の土地の地図を主題とするサイトですが、最長片道切符関連のページでは実在の駅名を扱っています。